In 2014, the Khan Academy had a cryptography challenge, called the 2014 Cryptochallenge. It consisted of a narrative leading to clues that were progressively more difficult to decode. The idea was to introduce people unfamiliar with ciphers and cryptography to some basic ciphering methods through examples and clues. I stumbled upon it well after it was debuted, but still had fun going through the challenge.
Please note that while I am displaying the code I wrote to decode the messages, and describe the methodology to arrive at the answers, I will not reveal the decoded messages because I don’t want to ruin the fun for others.
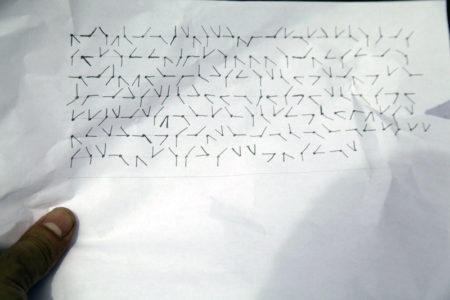
It all starts with the final clue, actually. In the challenge, the goal is to decipher this message that is found:
After finding out about a pair of burglars in the vicinity, you find a ciphered communique. The goal is to decode the message by finding clues left behind the pair of villains who communicate using various ciphers. Although this main message is the one we want to decode, we have to work through their previous communications in order to figure out the method of encoding.
Clue 1
The first clue is a simple cipher. Khan Academy gives us the clue that it is a Caeser Cipher, which is where the value of each letter is shifted n places. For example, we could encode the word “CAT” by shifting all the letters 3 values, and end up with “FDW”. Although easy to decode if you know the method, to someone who has no idea, it will just look like gibberish.
This is simple to brute force, as there are only 25 ways the shift the alphabet. I wrote the following C code to decipher the message in all 25 ways, and then I looked through the results for reasonable output.
void cipher(const char *input, char *output, int shift) {
for (int i=0 ; i<=strlen(input) ; i++)
if ('A' <= input[i] && input[i] <= 'Z') //Capitals
output[i]=(input[i]-'A'+shift)%26+'A';
else if ('a' <= input[i] && input[i] <= 'z') //Lowers
output[i]=(input[i]-'a'+shift)%26+'a';
else
output[i]=input[i];
}
int main(int argc, char *argv[]) {
const char *messageA="vwduwljudeehghyhubwklqjlfrxogilqgsohdvhuhwxuqdqbeoxhsulqwviruydxowdqgdodupghvljqedvhgrqzklfkedqnbrxghflghrqldpvhwwlqjxsvdihkrxvhfr";
const char *messageB="gluhflishjrvbadvyyplkaohavbyjpwolypzavvdlhrvuuleatlzzhnlzdpajoavcpnlulyljpwolyrlfdvykpzaolopkkluzftivsvmklhaoputfmhcvypalovsilpuluk";
for (int i=1 ; i<=26; i++) {
char outputA[strlen(messageA)];
cipher(messageA, outputA, i);
printf("1/2, Offset: %d\n%s\n\n", i, outputA);
char outputB[strlen(messageB)];
cipher(messageB, outputB, i);
printf("2/2, Offset: %d\n%s\n\n", i, outputB);
}
return 0;
}Clue 2
For this message, they give us the clue of Polyalphabetic Cipher. For this type of cipher, there is a key word that is repeated. Each letter of the alphabet is assigned a value based on it’s order (A=0, B=1… Z=25). The value of the key letter is added to the value of the message letter. If the value is greater than 25, you wrap the value around back to 0 and continue. From Wikipedia, we see this example:
Plaintext: ATTACKATDAWN Key: LEMONLEMONLE Ciphertext: LXFOPVEFRNHR
A (the 0th letter of the alphabet) plus L (the 11th), when added together would produce 11, which is L.
T (19th) plus E (4th) equals 23, which corresponds to X. Etc.
To reverse the cipher, all you need to do is subtract the values of the keyword from the scrambled text.
The key we will use was alluded to in the decoded first clue. For this clue, the cipher key was doubled; that is each letter of the word was used twice before advancing to the next letter. This is apparently a common practice. What tipped me off is that the thieves previous communication began with START, and ended with END. I presumed that they might do the same with this message. By subtracting the supposed value START from the scrambled message, I could confirm that the keyword was in fact doubled, and then plugged it into the program I wrote to decode the whole message.
void cipher(const char *key, const char *input, char *output) {
int n = 0; // Key index
for (int i=0 ; i<strlen(input) ; i++) {
int char_enc = input[i] - 'A'; // Get encoded char value
int char_key = key[n++ % strlen(key)] - 'A'; // get key char value
int char_dec = (26 + char_enc - char_key) % 26; // Reverse vigenere cipher
output[i] = char_dec + 'A'; // Store deciphered message
}
}
int main(int argc, char *argv[]) {
const char *code="SSKKUULLLL"; // Doubled letters for key is common
const char *message="KLKBNQLCYTFYSRYUCOCPHGBDIZZFCMJWKUCHZYESWFOGMMETWWOSSDCHRZYLDSBWNYDEDNZWNEFYDTHTDDBOJICEMLUCDYGICCZHOADRZCYLWADSXPILPIECSKOMOLTEJTKMQQYMEHPMMJXYOLWPEEWJCKZNPCCPSVSXAUYODHALMRIOCWPELWBCNIYFXMWJCEMCYRAZDQLSOMDBFLJWNBIJXPDDSYOEHXPCESWTOXWBLEECSAXCNUETZYWFN";
char output[strlen(message)];
cipher(code, message, output);
printf("%s\n", output);
return 0;
}Clue 3
Clue three was a tough one. I had to look up the hint, which points to a Kahn Academy video called “visual telegraph.” Within the video, we learn of a character encoding method called “Polybius Square.” It explains how characters can be communicated using pairs of numbers that describe a row and column in a character lookup table. Interestingly, in this clue, the message is composed entirely of numbers! We can assume that the table of characters is five by five in size because we never see any numbers smaller than one or larger than five. Additionally, we can also assume that the message starts with the word START again. This can help us figure out the orientation of the lookup table. I made a program to take pairs of numbers and print out the message using the table, and it worked like a charm!
void cipher(const char *input, char *output) {
char key[5][5]={{'A','F','K','P','U'},
{'B','G','L','Q','V'},
{'C','H','M','R','W'},
{'D','I','N','S','X'},
{'E','J','O','T','Y'}};
for (int i=0 ; i<strlen(input)-2 ; i=i+2) {
//Get coordinates from key grid
printf("%c",key[input[i]-'1'][input[i+1]-'1']);
//Save ascii to output
output[i]=key[input[i]-'1'][input[i+1]-'1'];
}
}
int main() {
const char *message="44541134541123335344541242434244325141212311311353155442544244424344325141534354324234411125513553341342432253431144543453432251343142143251341253341215541534513351444411225144425442444415345123551543213451111311212351425431533321424351445315341434512542531544335154325341443043513544";
char output[strlen(message)];
cipher(message, output);
printf("%s\n", output);
return 0;
}The Final Clue
The final clue stumped me for a while. I ended up getting busy and forgetting about the cryptochallenge. A few months later I found the files on my computer and resumed where I had left off.
Thanks to the previous messages, we found a “safe house” that yielded clues to how this final cipher was put together. Some key insights:
- The message is converted to digits using a method similar to clue 3
- There is a binary key which is obtained from a newspaper clipping where consonants are 0 and vowels are 1
- The symbols represent 2 digits; 1 digit for the vertical/horizontal and 1 digit for the diagonal positions




There were a lot of unknowns, and a few rounds of guess-and-check. One of the key distractions was thinking that each symbol was a letter. That is not the case! From the clues above, we can basically figure out that the process goes like this:
- Each letter first gets transformed into a 2 digit number using a Polybius Square (like clue 3).
- From there, the 2 digit number (values maxing out at 66) gets transformed to a 6 bit binary number.
- The binary number then gets logically XOR’d with the binary numbers produced by the newspaper article. (This is called the pad)
- The final binary gets split up into 3 bit chunks which get encoded into the final glyphs we found.
To successfully decode the message, we need to reverse the process. Looking at the clues, I made a guess as to what value the glyph positions indicated. After running the program, I didn’t get meaningful output, so I reversed them, and voila, it worked.
This time, I wrote the program in Python since Python is so much more forgiving with types.
The program first takes the pad text (the newspaper article) and converts it into binary.
I converted the glyphs to digits by hand, which was the most time consuming part. I separated the first digit and second digit into two different arrays. Vertical/horizontal lines are called ‘messageA’ and diagonal lines are called ‘messageB’.
I then convert these values sequentially into binary to create a “messagebin” array. Each value in the array gets XOR’d against the corresponding position’s value in the newspaper binary pad array. The result is processed 3 bits at a time and converted into an array of digits.
The list of digits is processed in pairs, and letters are looked up from a table. There was a clue showing that the table of letters was a clockwise spiral starting from the lower left. By adding digits to the spiral at the end, it worked out to fit perfectly in a 6 by 6 arrangement.
After some finagling, the program successfully deciphered the message! I was then able to thwart the would-be criminals!
def bin(x):
return ''.join(x & (1 << i) and '1' or '0' for i in range(1,-1,-1))
# Convert pad to binary
vowels = ["a","e","i","o","u","y"]
padbin = []
pad = "The whole-grain goodness of blue chip dividend stocks has its limits. Utility stocks, consumer staples, pipelines, telecoms, and real estate investment trusts have all lost ground over the past month, even while the broader market has been flat. With the bond market signalling an expectation of rising interest rates, the five-year rally for steady blue-chip dividend payers has stalled. Should you be scared if you own a lot of these stocks, either directly or through mutual funds or exchange-traded-funds? David Baskin, president of Baskin Financial Services, has a two-pronged answer: Keep your top-quality dividend stocks, but be prepared to follow his firm's example in trimming holdings in stocks such as TransCanada Corp., Keyera Corp., and Pembina Pipeline Corp. Lets have Mr Baskin run us through his thinking on divedend"
for c in pad:
if ord(c) < ord('A') or ord(c) > ord('z'): continue
if c.lower() in vowels :
padbin.append(1)
else:
padbin.append(0)
# Message based on pictograms
# 2 0 3
# \|/
# 3 - - 1 where straight lines are first digit (A)
# /|\ and slanted lines are second digit (B)
# 1 2 0
messageA = [2,3,2,2,0,3,3,0,0,2,2,0,3,2,1,3,0,3,0,3,0,0,2,0,3,2,
2,1,0,2,1,1,2,0,1,0,2,2,2,2,2,3,2,1,2,1,3,2,
3,3,0,2,2,1,1,1,0,3,2,1,2,0,0,1,3,0,3,2,3,0,1,
0,1,3,3,2,0,0,0,3,1,1,3,0,1,2,3,1,0,0,3,2,3,1,
0,0,0,0,3,0,2,2,3,1,0,1,2,0,0,1,3,0,1,1,2,0,2,0,
2,1,0,3,3,3,2,3,2,0,1,3,3,0,3,1,3,1,0,0,0,0,
2,2,0,3,2,0,2,2,3,2,0,0,3,2,2,1,3,0]
messageB = [0,3,2,1,0,3,0,1,2,0,2,2,2,0,1,3,3,0,3,2,3,0,2,1,3,3,
3,0,3,2,3,3,0,1,1,3,2,0,0,0,2,3,0,3,3,3,3,2,
0,3,1,0,1,0,2,1,0,2,3,3,2,2,0,0,1,2,3,0,1,3,2,
1,1,3,2,3,2,1,0,2,0,0,0,1,0,3,1,0,2,0,0,3,1,0,
3,3,1,2,3,2,3,1,0,2,3,2,2,0,3,3,1,0,0,1,1,3,3,2,
0,3,2,2,0,1,3,3,0,2,2,3,0,0,0,2,0,3,3,1,3,3,
3,2,2,0,0,3,2,3,2,3,2,2,1,0,3,3,0,2]
# Convert pictogram elements to binary
messagebin = ""
for i in range(len(messageA)):
messagebin += bin(messageA[i])
messagebin += bin(messageB[i])
# XOR pad and message together in binary
charcoords = []
tmp = ""
i = 0
while i < len(padbin) and i < len(messagebin):
tmp += str(padbin[i]^int(messagebin[i]))
# Set length of binary digits here (Probably 3 digit?)
if len(tmp) == 3:
charcoords.append(int(tmp, 2))
tmp = ""
i += 1
# Convert message from binary to alphabet based on Polybius square
key = [["F","G","H","I","J","K"],
["E","X","Y","Z","0","L"],
["D","W","7","8","1","M"],
["C","V","6","9","2","N"],
["B","U","5","4","3","O"],
["A","T","S","R","Q","P"]]
for i in range(0, len(charcoords)-1, 2):
if charcoords[i] > 5 or charcoords[i+1] > 5:
print "?",
else:
print key[charcoords[i]][charcoords[i+1]],
This was a very enjoyable exercise, and taught me some basics about ciphers (and patience). I hope they put on similar exercises in the future!