Coastal Vectors

Cookie Crawl

Where we live, there is an abundance of bakeries that just sell cookies. I don’t get it as I’d rather just bake my own cookie at home. My wife however likes these oversized cookies and their many novelty flavors. For her birthday, I decided to take her and the family to many of these establishments in order to decide once and for all which was the superior cookie making establishment.

For this endeavor, I created a rubric for scoring each cookie based on flavor, aroma, bake, etc. You can find it here:

Each member of the family filled one out. We got 2 cookies from 5 different bakeries; 10 cookies to evaluate in total.

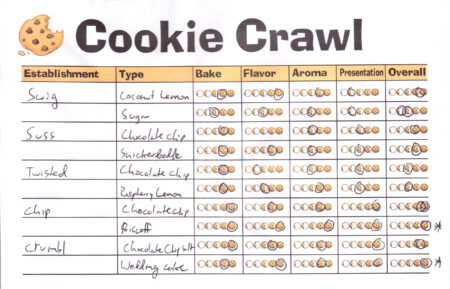
Here is the example of how I scored the different cookies:

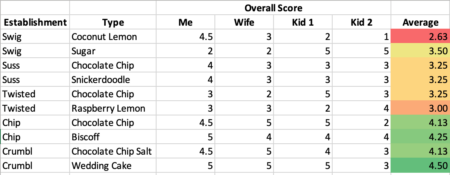
Here are the tabulated results for our quest (for those who bothered to fill out the rubric).

In the end, it was a fairly conclusive victory for Crumbl. In particular, the Wedding Cake cookie they were sporting this week was well regarded by all. The worst was Swig; in particular the Coconut Lemon was only liked by me.

Make of that what you will, but we had fun consuming far too many calories worth of cookies in one day!

Finding Old Video Game Music

The other day my sister left me a voice mail hoping I could help her identify a tune she had in her head. She sang it and I instantly recognized it. I couldn’t remember where it was from, but I had the vivid recollection that it was from a game we played as kids.

I was also pretty certain it was a game we played on our Macintosh. I mentally went through some of the games we played a lot, and then it hit me; it was from Spectre VR!

Spectre was vector tank game where you have to collect flags while avoiding or destroying enemy tanks. It was available on many platforms. My first attempt to find the music track was to download MIDI files from a website that had collections of old video game music. I think these files were taken from the DOS version or some other platform, and none of them sounded quite right.

I decided to run the original game in my SheepShaver Mac OS 9 emulator to verify that this game was indeed the correct one. Bingo. Level 2 has the music in question!

The next thing I did was get a copy of ResForge (this is a forked version of ResKnife which is no longer in development). ResForge is an editor/viewer for old OS 9 resource forks. Back in the day, you could look at resource forks using ResEdit. Using ResForge, I was able to locate and export all the MIDI files from my original copy of Spectre.

The problem with MIDI files is that they only sound correct if they have the correct instruments, and unfortunately, the instruments (samples) were kept in a different resource. So the MIDI files didn’t sound right. I used the same program to export all the sampled instruments, and identified which ones were used for this music.

Example instrument (vibraslap):

I used Garage Band to import the MIDI track and then assigned a sound sampler to each voice. I loaded the appropriate sample into each one. For some reason I had to transpose a few of the samples to get it sounding just right.

Here is the final track:

If you compare it to the in game music capture, it sounds perfect. Kind of a silly diversion, but nostalgia can be intoxicating! What games from your childhood had memorable music?

Oh man. This music is going to be in my head all day…

Creating a 150 Year Old Soap Box

Have you ever heard of ACME soap? I can’t say definitively if the company still exists, but it was a soap brand from the early 1800’s. Growing up, my grandma’s bathroom was wallpapered with ACME Soap themed wall paper. It had various advertisements, pictures, logos, etc all representing the ACME Soap brand. I have memories of looking at the various artwork while doing my business there.

One of the most memorable ones was a four panel story of a boy that falls in a well. He is holding a bar of ACME Soap, and it lathers up so much that it lifts him to the top, thus saving him. Below are the four panels as seen in the official trading cards.

When the bathroom got remodeled, each grandchild was gifted this four panel advertisement framed for us to put in our own bathrooms, which we did.

I felt that the picture frame looked a little lonely on its own, and thought that making a soap box to accompany it would be appropriate. Although not at all historically accurate, I took the dimensions of a modern soap box, and styled it appropriately.

I found a graphic that was actually used on the antique soap boxes that depicts a man holding a bar of soap. I recreated the ACME logo and added some verbiage and legal text that I could find on various images of their products. According to what I found they were founded in 1811, and the trademark was registered in 1875.

I used an old paper texture to make it look more aged.

I printed it out on card stock, cut it out, and glued it up.

Now it sits and complements the original wall paper that sits on display in the bathroom.