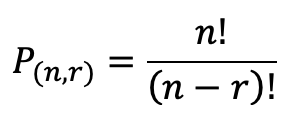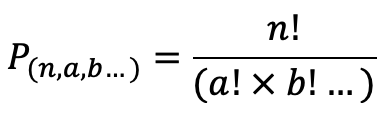Coastal Vectors

Project Euler 43

I like to go back and re-solve Project Euler problems in different languages. Lately, I’ve been solving them in Javascript for fun. When I do this, I don’t look at previous solutions and try to do it from scratch. When I was finished, I was surprised by the performance of my solution to 43 compared to my previous attempts in other languages.

Problem 43 is as follows:

The number, 1406357289, is a 0 to 9 pandigital number because it is made up of each of the digits 0 to 9 in some order, but it also has a rather interesting sub-string divisibility property.

Let d₁ be the 1^st digit, d₂ be the 2^nd digit, and so on. In this way, we note the following:

d₂d₃d₄=406 is divisible by 2

d₃d₄d₅=063 is divisible by 3

d₄d₅d₆=635 is divisible by 5

d₅d₆d₇=357 is divisible by 7

d₆d₇d₈=572 is divisible by 11

d₇d₈d₉=728 is divisible by 13

d₈d₉d₁₀=289 is divisible by 17

Find the sum of all 0 to 9 pandigital numbers with this property.

When I first solved this problem, I solved it in C. This was in 2014, and I was still fairly green. My solution at the time was to iterate through every 10-digit number and see if it was pandigital and then if it was, check if it met the sub-divisibility requirement.

This solution is what you would call “brute-force”. It’s inelegant, and slow. However, it does work. It took 33.948 seconds to compute.

A few years later I was doing more with Rust and Python. Both of these solutions I created used the same method. This probably happened because I wrote both solutions close together. At any case, this time I thought myself more clever and took a pandigital number, 1234567890, and discovered every permutation, and then checked for the sub-divisibility requirement of each.

This is better than brute force, but still time consuming. Python can accomplish this in 18.724 seconds and Rust in 4.621. Better, but still not great.

The general rule of thumb with Project Euler is that if a solution takes more than a second, you haven’t found the intended method of solving it.

Looking at it this time around, it seemed like a very straightforward problem with an obvious path for a solution. Instead of finding pandigital numbers and checking if they meet the sub-string divisibility requirement, this time I would build up the pandigital numbers using the sub-strings.

First I created arrays for the multiples of the first 7 primes with 2 and 3 digits. I then used a recursive function to build up a number using valid combinations of these sub-strings (since each one overlaps the next with 2 digits). This creates a much smaller group of numbers to check.

Once I have all my potential pandigital numbers, I check to make sure they are in fact pandigital. (Note that at this stage, they should be missing the first digit). When checking for pandigitality, I’m actually looking for 9 different digits, and if so, I prepend the missing 10th digit and voila, it’s a valid pandigital number!

This solution is much, much faster at .237 seconds.

I’m very pleased with that result, but a little shocked I didn’t see this method when I have solved it previously. It’s nice to know that since I first started solving these problems years ago, I can see measurable improvement in my ability to find and create solutions to these fun little puzzles.

Source on GitHub

Project Euler 117

I enjoy solving Project Euler problems in my downtime. Problem 117 is one that I’ve looked at multiple times, but never came up with a good solution. The premise is easy enough, but, as with most Euler problems, the scale of the problem presents issues.

Using a combination of grey square tiles and oblong tiles chosen from: red tiles (measuring two units), green tiles (measuring three units), and blue tiles (measuring four units), it is possible to tile a row measuring five units in length in exactly fifteen different ways.

How many ways can a row measuring fifty units in length be tiled?

For the context of my solution, I am representing the tiles as an array or list of integers that each represent the length of a tile. For example, (1, 3, 1) would be a black, green, and black tile taking up a total of 5 spaces.

Brute Force sometimes works on these problems, but more often than not, they take far too long to complete. I don’t feel like I’ve “solved” one of these problems if the solution takes more than a second or two. My first naive attempt to solve this problem was to attack it recursively and build all the combinations of tiles. After letting it run for a few minutes, I gave up and assumed there must be a better way.

While building each tile combination was prohibitively time consuming, I found that I could still use recursion to get the base combinations for the tiles. There are only about 1000 of those, so the trick will be permuting them to get the full count. Well, as it turns out, this led to a few more problems.

Using the permutations tool provided in itertools proved to be too slow as well. First of all, it was finding too many solutions. For example:
>>> for i in list(itertools.permutations([1, 1, 2, 2])): print i ... (1, 1, 2, 2) (1, 1, 2, 2) (1, 2, 1, 2) (1, 2, 2, 1) (1, 2, 1, 2) (1, 2, 2, 1) (1, 1, 2, 2) (1, 1, 2, 2) (1, 2, 1, 2) (1, 2, 2, 1) (1, 2, 1, 2) (1, 2, 2, 1) (2, 1, 1, 2) (2, 1, 2, 1) (2, 1, 1, 2) (2, 1, 2, 1) (2, 2, 1, 1) (2, 2, 1, 1) (2, 1, 1, 2) (2, 1, 2, 1) (2, 1, 1, 2) (2, 1, 2, 1) (2, 2, 1, 1) (2, 2, 1, 1)
When in reality many of those are equivalent in the terms of the problem conditions. What we want is a set which looks more like this:
>>> for i in set(itertools.permutations([1, 1, 2, 2])): print i ... (1, 1, 2, 2) (2, 1, 2, 1) (2, 1, 1, 2) (1, 2, 2, 1) (1, 2, 1, 2) (2, 2, 1, 1)
That works, but the program still has to calculate all the permutations that we are throwing out which is time consuming; at the most, a set will have 50 tiles which is 50! permutations. That’s 30414093201713378043612608166064768844377641568960512000000000000 permutations, which is really just an insane amount! So that won’t do.

Well, we don’t need to know the permutations, just the amount of permutations! Let’s see if we can find a formula for that. The general formula that I found which researching permutations looks like this:

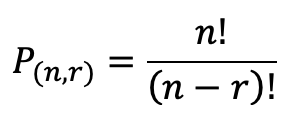
where n is the number of terms, and r is the number of terms you are choosing from your source pool. In this case, we are going to always use all the tiles in our base combination that we want to permute, so the number of permutations is just the factorial of the number of tiles. Hmm. That doesn’t really help since it doesn’t filter out any duplicates.

Perhaps if I researched a bit more, I could have found the proper formula for this situation. Rather than read more about permutations, I decided to take one of my base combinations and do some experiments to see if I could derive a formula for this situation. I took the last combination from my list and computed the number of unique permutations in order to see what my goal should be. (This operation took over 10 minutes)
>>> print len(set(itertools.permutations([3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4]))) 78
I played around with factorials and found that for my 13 terms there would be 13!, or 6227020800, possible permutations. Since I knew I wanted the formula to result in 78, I divided the number of permutations by 78 and got 79833600. In theory, this number would be the denominator of my not-yet-existent formula. I tried grouping my 3s and 4s together; there are 2 and 11 respectively. I checked what 11! is and it turned out to be 39916800 which is exactly half of my target value for the denominator. And 2! (for the number of 3s) is 2. That seems pretty promising!

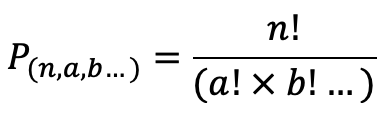
My hypothesis was that multiplying the factorials of the number of similar terms together and then dividing them into the number of possible permutations would yield my desired result. I tested it out on another combination and it worked out correctly, so I modified my program to perform this operation on each combination. I ran it and checked the answer, and it was correct!

And it only took .083 seconds! I’m pretty happy with the results. I’m sure a mathematician might have a more clever, direct way of solving this problem, however I think that since this solution is accurate and quick I can be proud of it. You can see the complete code on my github.

Making USB Bootable Windows 10 Installer

I needed to update some servers to Windows 10/2016 at work this week, but didn’t have any DVDs large enough to accommodate the 5.8 GB size of the Windows ISO. Normal DVD+Rs are 4.7 GB, so to make use of the ISO I downloaded from MSDN, one needs a DVD-R DL which can hold 8.5 GB of data.

I didn’t feel like going to a store or waiting for delivery, so I used Microsoft’s “Windows 7 USB/DVD Download Tool” (seemingly misnamed since it supports windows 7 and newer).

Once downloaded, the tool is fairly straight forward. You point it to an ISO, and then to a USB drive, and voila, it copies the data.

The annoyance is that I got the error “We were unable to copy your files. Please check your USB device and the selected ISO file and try again.” Trying again, of course, did not resolve the issue.

Fortunately, someone knowledgeable was able to explain the root cause of the error. The USB’s MBR needs to be cleared. This doesn’t happen automatically with the Windows Download Tool.

To clear the MBR and format the drive, follow these steps using the diskpart tool:

diskpart
diskpart> list disk
diskpart> select disk #
diskpart> clean
diskpart> create partition primary
diskpart> select partition 1
diskpart> active
diskpart> format quick fs=fat32
diskpart> assign
diskpart> exit

This resolved my issue and I was able to go along my merry way.

I don’t use Windows a lot in my every-day life, but it is something I use quite a bit at work. Documenting little things like this helps me to remember tricks I come across, and hopefully can help other people searching for solutions to similar problems.