Math can be beautiful. One of the mathematical things that has always intrigued me has been the visualization of the Mandelbrot set. I never tried to generate it myself until just recently. The only understanding I had previously of the Mandelbrot set was vague. I looked for some explanation on how to do the computation, but I couldn’t find an adequately succinct explanation. My brother helped me take the Mandelbrot equation and massage it into an understandable format that I could then plug into a program to generate my own image of the Mandelbrot set.

Generating the Mandelbrot set is straight forward once you understand what the Mandelbrot set really is. The fractal depicts a grid of coordinates along the x and y axis that either fall into the set or not. The formula gets computed using the x and y position for the pixel in question, and then the resulting number get put back into the equation. The resulting number either gets larger or smaller. If it passes a certain threshold, then we decide it is not a part of the set, and move on. The resulting image is a bit map of numbers that are either part of the Mandelbrot set, or not. The fun gradients and colors, with which we are all familiar, represent how many times the calculation had to be performed before the number passed the threshold.

The Mandelbrot equation is as follows, where z_(n+1) is the value for which we are solving, (z_n)² is our accumulated value so far, and C is our complex coordinate.

z_(n+1) = (z_n)² + C

We are just focusing on the right side of the equation for now, because the left contains the values that we want to solve for. Let’s expand the right side of the equation with complex coordinates so we can simplify the answer.

= (x′ + y′ × i)² + x + y × i

The next step is to expand the accumulated value. We can use our old friend FOIL.

= x′² + 2(x′ × y′ × i) + (y′ × i)² + x + y × i

The i² simplifies down to -1, reducing the number of imaginary numbers to worry about.

= x′² + 2(x′ × y′ × i) – y′² + x + y × i

Next we will move all the components with an imaginary number (i) to the right.

= (x′² + x – y′² )+( 2(x′ × y′ × i) + y × i)

Now we can the simplify by isolating the i.

= (x′² + x – y′²)+(2 × x′ × y′ + y) × i

Now the right side of the equation resembles a complex coordinate, which happens to be what we are solving for on the left.

x′′ + y′′ × i = …

So, each element of the left hand side of the equation can be solved with its counterpart element on the right.

x′′ = x′² + x – y²

y′′ = 2 × x′ × y′ + y

i = i

Since the i is equal to i, and remains independent from the rest of the variables, we can just ignore it.

Now, all we need to do is plug x and y to generate our new x′′ and y′′, and then keep plugging in the new values until the numbers go out of bounds, or we reach our threshold.

With the equation in hand, I started out by prototyping the program in Python, and outputting a Portable PixelMap (PPM) file because it is a dead-simple file format. When I first ran the program, it generated this image:

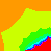
I was really disappointed that I didn’t get a meaningful image the first time I ran it. I verified the equation I was using, and the basic logic of the code, but it still came out like this. I kicked up the threshold a little bit to see what would happen, and suddenly I realized what the problem was. I was only rendering the upper left quadrant of the image. I finagled the bounds of the image, and ended up with the recognizable shape here:

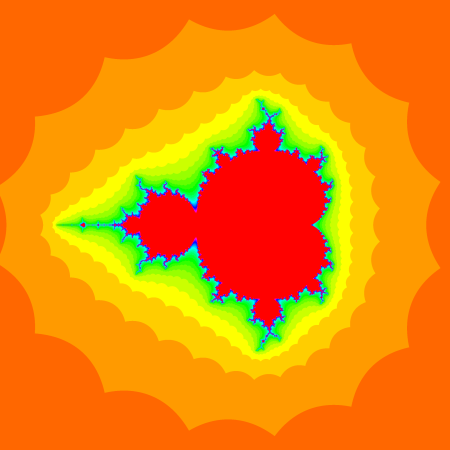
This certainly looked better, but something was still off. In all the Mandelbrot images I had seen, the different threshold levels looked smooth and curved, not jagged like mine were looking. It turned out I had misunderstood how to check if the calculation was out-of-bounds. This code is the culprit:

if (abs(xT) + abs(yT)) > 10:

This is the conditional statement that decides whether the number has fallen out-of-bounds. The key is to check if the number has left the circular area that contains the entire Mandelbrot set, which has a radius of 2. This would mean that the enclosing circle is something like x′′² + y′′² = 2². The corrected out-of-bounds check looks like this:

if ((xT**2) + (yT**2)) > 4:

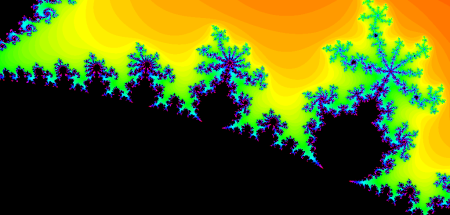
With that change, the images started coming out beautifully. With that, I started adding in command line options to set the bounds of the image, the depth, the gradient colors, etc. in order to easily render custom images of the set.

Now that I did it all in Python, I decided I should do it in C. Rendering 1024 pixel square image in Python takes about 15 seconds. To compare, rendering the same image in C takes .1 seconds; substantially faster!

The following code from my function, mandel(), calculates whether any given point is in the Mandelbrot set. The function takes an x and a y coordinate, and the threshold level which I call “depth”. It returns a -1 if the number is in the set, or it will return an integer representing the number of iterations it took for the point to become out-of-bounds.

int mandel(double x, double y, int depth)
{
    double xP=0, yP=0; // Prime Values
    double xT=0, yT=0; // Temporary Values
    int i=0;
    for (i=0; i<depth; i++)
    {
        xT = (pow(xP, 2)) + x - (pow(yP, 2));
        yT = 2 * xP * yP + y;
        if (pow(fabs(xT),2) + pow(fabs(yT),2) > 4)
            return i;
        xP = xT;
        yP = yT;
    }
    return -1;
}

The current code for both the Python and C versions are available from my GitHub page.

I was recently going through some old Project Euler solutions, and noticed that my solution to problem 12 was never optimized. The problems asks:

The sequence of triangle numbers is generated by adding the natural numbers. So the 7^th triangle number would be 1 + 2 + 3 + 4 + 5 + 6 + 7 = 28. The first ten terms would be:

1, 3, 6, 10, 15, 21, 28, 36, 45, 55, …

Let us list the factors of the first seven triangle numbers:

1: 1
3: 1,3
6: 1,2,3,6
10: 1,2,5,10
15: 1,3,5,15
21: 1,3,7,21
28: 1,2,4,7,14,28

We can see that 28 is the first triangle number to have over five divisors.

What is the value of the first triangle number to have over five hundred divisors?

The way I originally solved this problem was a brute-force approach following this basic logic:

1. Calculate next triangle number
2. Try dividing number by every integer smaller than the number
3. Count the number of integers that divide evenly
4. Go to step 1 and repeat until divisors are greater than 500

This process yielded the results, but it is far from elegant or optimized. it took 14 minutes to calculate the answer! I knew that dividing by each number was a waste; there had to be a better way.

Although I didn’t know it, I felt fairly certain that there was a relationship between prime factors and the number of divisors. It turns out I was right. There is a trick to calculate the number of divisors if you know the prime factors.

Using the number 28 as an example, we can find that the prime factors are 2, 2, and 7, which can be written as 2² × 7¹. Interestingly, if we take the exponents, add 1 to each, and then multiply them together, we can calculate the number of divisors. For this example, this becomes (2+1) × (1+1), which is 2 × 3, which equals 6. (This is also mentioned in the Wikipedia article for divisor briefly in the section titled ‘Further notions and facts’).

Equipped with this knowledge, I was able to devise a more efficient method to solve this problem:

1. Pre-calculate primes up to x amount (to save effort recomputing each time)
2. Calculate next triangle number that is divisible by 3 or 5 (I found a pattern that the most divisible triangle numbers were divisible by 3 or 5)
3. Go through primes and divide number by primes until number equals 1
4. Convert the prime factors to divisors
5. Go to step 1 and repeat until divisors are greater than 500

While this method is more complex, it yielded great results. Once I was done refining this method, I got the compute time down to .086 seconds. That is a very substantial improvement!

The interesting part of the code is the findDivisors function, seen below.

int findDivisors(int input, int *primes, int primesToFind)
{
    int i, count=1;
    int primeCount[primesToFind];
    for (i=0; i<primesToFind; i++)
    primeCount[i] = 0;

    // Prime factorization
    while (input != 1)
        for (i=0; i<primesToFind; i++)
            if (input % primes[i] == 0)
            {
                input = input / primes[i];
                primeCount[i]++;
            }

    // Convert prime factorization to divisors
    for (i=0; i<primesToFind; i++)
        if (primeCount[i] > 0)
            count *= (primeCount[i]+1);

    return count;
}

In this function, the inputs are:

• The triangle number (input)
• The array of pre-calculated prime numbers (primes)
• The number of primes in the array (primesToFind)

As the division of primes occurs, I keep track in a separate array (primeCount) how many times a given prime index is used to divide. This keeps track of the prime factorization I talked about earlier so we can finally compute the number of divisors. Once computed, we pass back the count, and the program moves on to the next triangle number.

So there you have it. My entire solution is available on my GitHub page.