Coastal Vectors

EV Charging Stalls Vision Recognition

At the office, we have 12 parking stalls that provide free charging for electric vehicles. This is a nice perk, but unfortunately, there are a lot of EV owners. Finding a parking stall can be very difficult! Someone has thought of this, and very kindly placed cameras looking down on the stalls from the 4th floor so that those interested can see if any chargers are available without leaving the comfort of their desk.

I find having to check the cameras to be a bit of a burden though, so I thought it would be a good excuse to learn a bit more about computer vision by writing a small program to detect open stalls automatically, and notify me. I’ve never really done much in this area and thought it would be interesting.

Machine Learning

Using some sort of LLM seemed like the most obvious approach. I used the ultralytics library in Python and tried it’s built model which didn’t do great.

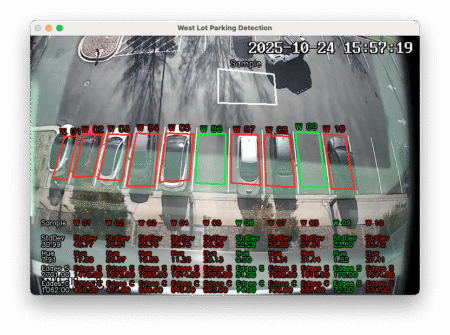
I thought a more tailor-made model would perform better. I looked on roboflow for models that were trained on aerial photography of parking lots. I uploaded a screenshot to multiple models and found the one with the best performance.

The model seemed to do pretty well, however it was having troubles detecting cars on the very edges. I suspect this is because of the skewed geometry from the lens distortion, but I’m not really sure. I also had a lot of overlapping results and false positive and false negatives.

I tried optimizing it using a few different methods. I tried cropping the image down to the bare minimum so that there was less to distract the LLM when looking for predictions. This didn’t help the edge stalls in being detected.

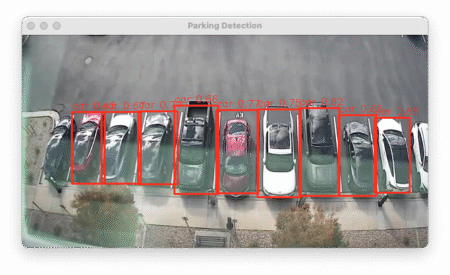I also tried cropping each stall individually and running the model on each independently. This made results even worse! I was now getting a lot of false positives on the parking stripes and false negatives on cars. No effect on the far left stall either.

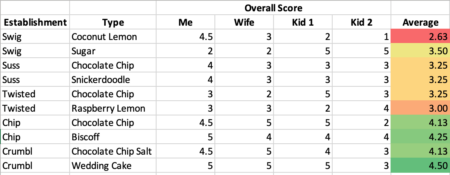
I left it running and started saving screenshots periodically as well as what the predictions are. During this time, I captured 141 images and predictions. Of those, 52 were not accurate predictions.

Accuracy: 63%

That was a lower accuracy than I was hoping for. I had a couple ideas on how to move from here. One is to collect images for a long enough time to train my own model. Ideally, I’d want to do this after collecting samples for a year in order for all possible seasons and lighting conditions to be included.

The second idea is to go more low-tech, and look into traditional image analysis techniques.

Traditional Image Analysis

For doing image analysis I used the Python library, cv2 along with numpy.

Average Color Detection

One method is to take the average color for a sample area of asphalt and compare against the average color in each parking spot and see how different they are. This is an easy check to implement, but there are many way in which this can fail. For example: Shadows, wet asphalt, car driving through sample area, grey cars.

Unsurprisingly, this was a fairly abysmal result. It could probably be tuned a bit, but I don’t think it would ever be viable.

Accuracy: 25.78%

Pixel Brightness Uniformity

By looking at the pixel brightness and getting the standard deviation, we can see how uniform the pixels in an area are. Asphalt is fairly uniform, but a car with windows and paint, and glare are not very uniform. This is also pretty easy to implement, and works fairly well. This method also has similar pitfalls to the previous method; Shadows, wet asphalt, and cars that are low contrast colors.

Accuracy: 51.92%

Hue Uniformity

Another method is to look at the hue uniformity. My goal here was to eliminate the issue of shadows, this way a parking spot half in light and half in shadow would have a higher uniformity than a car which has features/windows etc. Similar issues apply here as well, such as dull-colored cars, bad lighting.

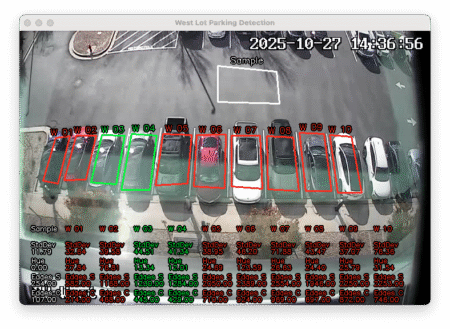This ended up being a huge step backwards at only identifying 229 of my 630 images correctly.

Accuracy: 36.35%

Edge Detection

Rather than looking at color uniformity, or brightness uniformity, what if we looked for image uniformity by detecting edges? This is also easy to implement in Python using the cv2 library. After dialing in a threshold, the accuracy was astoundingly good. It’s particular weakness is where there are intricate shadows or splotchy textures from rain/water. False negatives are less likely than false positives.

Accuracy: 95.57%

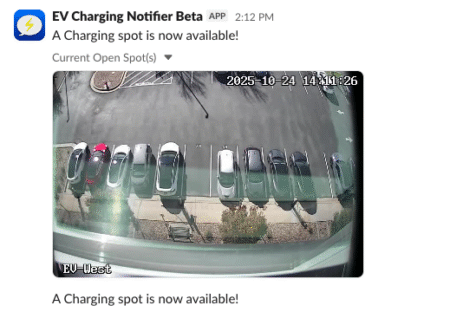
Notifications

The final step was to create a Slackbot that would notify me when a parking spot becomes available. I had never done this before, so I followed a tutorial.

I limited my Python script to only send notifications on work days and during normal work hours. It also only notifies me when it goes from no spots available to 1 or more spots available.

Conclusion

The system is working well enough in it’s current state. I intend to revisit this project in a few months after we get into winter. I suspect that the current edge detection method will fail when we start having snow on cars. I am saving screenshots periodically in order to build up training data to attempt creating my own model for this particular problem. In the mean, I should be able to charge at work more often!

Cookie Crawl

Where we live, there is an abundance of bakeries that just sell cookies. I don’t get it as I’d rather just bake my own cookie at home. My wife however likes these oversized cookies and their many novelty flavors. For her birthday, I decided to take her and the family to many of these establishments in order to decide once and for all which was the superior cookie making establishment.

For this endeavor, I created a rubric for scoring each cookie based on flavor, aroma, bake, etc. You can find it here:

Each member of the family filled one out. We got 2 cookies from 5 different bakeries; 10 cookies to evaluate in total.

Here is the example of how I scored the different cookies:

Here are the tabulated results for our quest (for those who bothered to fill out the rubric).

In the end, it was a fairly conclusive victory for Crumbl. In particular, the Wedding Cake cookie they were sporting this week was well regarded by all. The worst was Swig; in particular the Coconut Lemon was only liked by me.

Make of that what you will, but we had fun consuming far too many calories worth of cookies in one day!

Project Euler 43

I like to go back and re-solve Project Euler problems in different languages. Lately, I’ve been solving them in Javascript for fun. When I do this, I don’t look at previous solutions and try to do it from scratch. When I was finished, I was surprised by the performance of my solution to 43 compared to my previous attempts in other languages.

Problem 43 is as follows:

The number, 1406357289, is a 0 to 9 pandigital number because it is made up of each of the digits 0 to 9 in some order, but it also has a rather interesting sub-string divisibility property.

Let d₁ be the 1^st digit, d₂ be the 2^nd digit, and so on. In this way, we note the following:

d₂d₃d₄=406 is divisible by 2

d₃d₄d₅=063 is divisible by 3

d₄d₅d₆=635 is divisible by 5

d₅d₆d₇=357 is divisible by 7

d₆d₇d₈=572 is divisible by 11

d₇d₈d₉=728 is divisible by 13

d₈d₉d₁₀=289 is divisible by 17

Find the sum of all 0 to 9 pandigital numbers with this property.

When I first solved this problem, I solved it in C. This was in 2014, and I was still fairly green. My solution at the time was to iterate through every 10-digit number and see if it was pandigital and then if it was, check if it met the sub-divisibility requirement.

This solution is what you would call “brute-force”. It’s inelegant, and slow. However, it does work. It took 33.948 seconds to compute.

A few years later I was doing more with Rust and Python. Both of these solutions I created used the same method. This probably happened because I wrote both solutions close together. At any case, this time I thought myself more clever and took a pandigital number, 1234567890, and discovered every permutation, and then checked for the sub-divisibility requirement of each.

This is better than brute force, but still time consuming. Python can accomplish this in 18.724 seconds and Rust in 4.621. Better, but still not great.

The general rule of thumb with Project Euler is that if a solution takes more than a second, you haven’t found the intended method of solving it.

Looking at it this time around, it seemed like a very straightforward problem with an obvious path for a solution. Instead of finding pandigital numbers and checking if they meet the sub-string divisibility requirement, this time I would build up the pandigital numbers using the sub-strings.

First I created arrays for the multiples of the first 7 primes with 2 and 3 digits. I then used a recursive function to build up a number using valid combinations of these sub-strings (since each one overlaps the next with 2 digits). This creates a much smaller group of numbers to check.

Once I have all my potential pandigital numbers, I check to make sure they are in fact pandigital. (Note that at this stage, they should be missing the first digit). When checking for pandigitality, I’m actually looking for 9 different digits, and if so, I prepend the missing 10th digit and voila, it’s a valid pandigital number!

This solution is much, much faster at .237 seconds.

I’m very pleased with that result, but a little shocked I didn’t see this method when I have solved it previously. It’s nice to know that since I first started solving these problems years ago, I can see measurable improvement in my ability to find and create solutions to these fun little puzzles.

Source on GitHub