Coastal Vectors

Revolutionizing the Bicycle

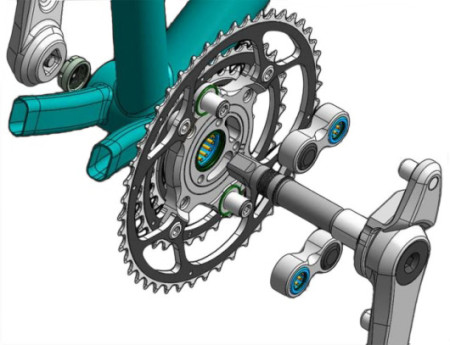
I had a great idea a few months ago. It was simply brilliant. It would revolutionize the way we bike. I couldn’t find anything like the idea that I had pictured in my head, and my brain immediately began racing with possibilities of prototyping this idea, patenting it, kickstarting it, and starting a business.

I quickly enlisted the help of a friend with a lot of experience with mathematics and mechanical expertise. Obviously, the idea sounds great to him too, and we started searching for away to accomplish what we are envisioning.

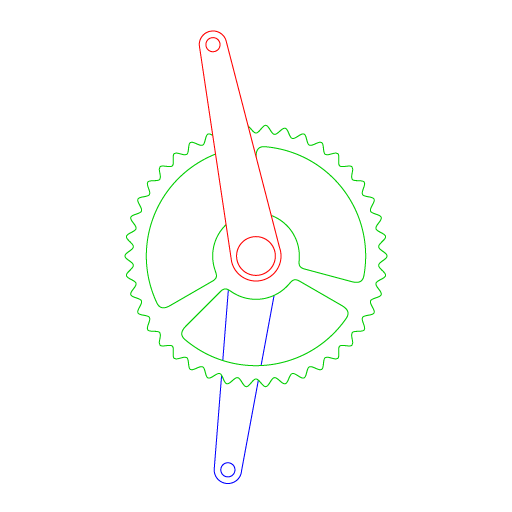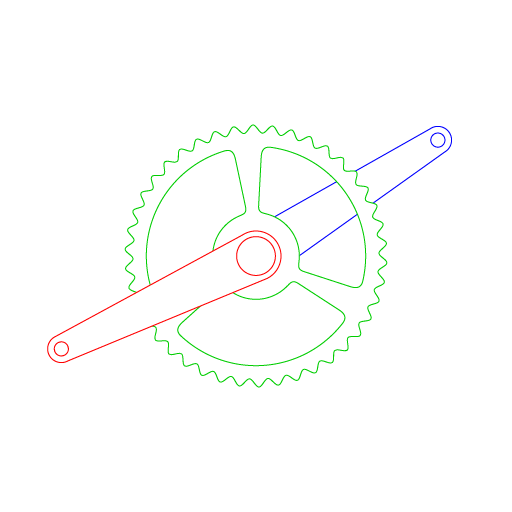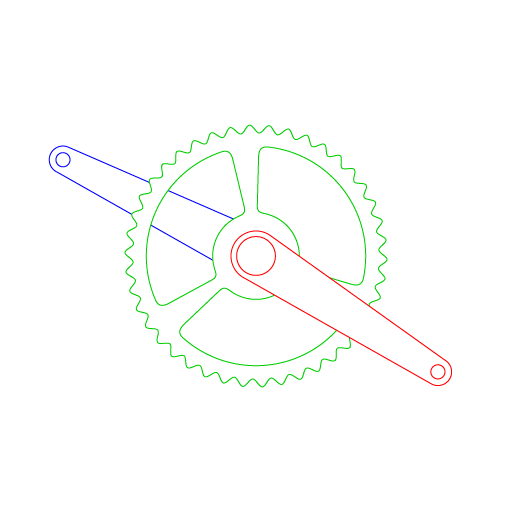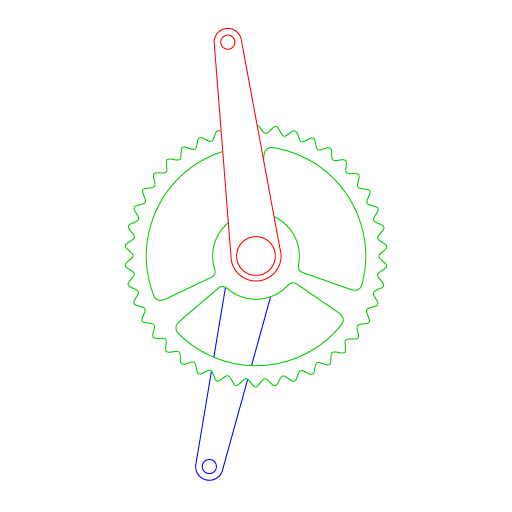The crux of the idea is to reduce wasted motion when peddling, allowing the cyclist to apply energy to his forward momentum more consistently and evenly. To accomplish this, I wanted to create a system where the crank arms do not move at a constant (linear) speed around the crank. This requires the left (red) and right (blue) crank arms to be independent from each other, but synced in their motion. This also requires a some type of gear mechanism that allows the crank gear (green) to move uniformly.

Having achieved all this, the result would be a motion where the leg spends more time pushing down in the front of the peddling motion than recovering on the upswing part of the motion. My theory was that eliminating the dead spot completely, and always having one foot in a power position, that cycling would be more efficient in terms of power applied over time.

We got to work thinking the problem through in our heads, and what the mechanism would have to be like. We at first looked at non-circular gears, but that turned out to not be feasible. Eventually we looked at planetary gear systems, but that was also very complicated. Every path we took though seemed to have a dead end, or so complicated that it seemed impractical.

Then it happened. My friend stumbled upon a company that had already invented this device. It’s called the RS4X (review of RS4X by Gizmag from 2005), and is made by a company called Rotor Bike Components. One of the reasons we didn’t come across this product during our preliminary research is that the company stopped selling them in favor of Q-Rings, or non-cricular crank gears. The company was actually founded around this idea in 1999.

What’s surprising though, is that they were not the first. A patent exists for this same design from the 1970’s. A man named Tom Traylor created the design, and applied for a patent. Unfortunately, he was not granted the patent (and unfortunately lost his $2000 filing fee). Similar ideas, it turns out, had been patented no-less than 5 times within the last 100 years, the oldest being an English patent from the 1870’s with a nearly identical implementation to Tom’s, and Rotor’s. Tom made a little write-up about his experience that appeared in Recumbent Cyclist News in 2004, which can be read here.

In the 1800’s, mechanical system were all the rage. It’s what people researched, designed, and tinkered with back in the day. It shouldn’t be surprising that this idea had already been explored so many times during the last century.

So why didn’t it catch on? I don’t have any definite reasons, however I have some theories.

The added complexity of the mechanics lends itself to more frequent malfunctions and failures.
The benefit is outweighed by the propensity of mechanical failure.
The advantages of such a system are actually negligible in practice.
The mechanism is too costly for mainstream usage.

Whatever the reason, the truth is that the idea just hasn’t taken off. I’d still like to try one to see what its like though. It was fun to think about. I suppose the real take away is that it’s hard to come up with a completely new, unexplored idea, but if you ever do, jump on it!

Project Euler 12

I was recently going through some old Project Euler solutions, and noticed that my solution to problem 12 was never optimized. The problems asks:

The sequence of triangle numbers is generated by adding the natural numbers. So the 7^th triangle number would be 1 + 2 + 3 + 4 + 5 + 6 + 7 = 28. The first ten terms would be:

1, 3, 6, 10, 15, 21, 28, 36, 45, 55, …

Let us list the factors of the first seven triangle numbers:

1: 1
3: 1,3
6: 1,2,3,6
10: 1,2,5,10
15: 1,3,5,15
21: 1,3,7,21
28: 1,2,4,7,14,28

We can see that 28 is the first triangle number to have over five divisors.

What is the value of the first triangle number to have over five hundred divisors?

The way I originally solved this problem was a brute-force approach following this basic logic:

Calculate next triangle number
Try dividing number by every integer smaller than the number
Count the number of integers that divide evenly
Go to step 1 and repeat until divisors are greater than 500

This process yielded the results, but it is far from elegant or optimized. it took 14 minutes to calculate the answer! I knew that dividing by each number was a waste; there had to be a better way.

Although I didn’t know it, I felt fairly certain that there was a relationship between prime factors and the number of divisors. It turns out I was right. There is a trick to calculate the number of divisors if you know the prime factors.

Using the number 28 as an example, we can find that the prime factors are 2, 2, and 7, which can be written as 2² × 7¹. Interestingly, if we take the exponents, add 1 to each, and then multiply them together, we can calculate the number of divisors. For this example, this becomes (2+1) × (1+1), which is 2 × 3, which equals 6. (This is also mentioned in the Wikipedia article for divisor briefly in the section titled ‘Further notions and facts’).

Equipped with this knowledge, I was able to devise a more efficient method to solve this problem:

Pre-calculate primes up to x amount (to save effort recomputing each time)
Calculate next triangle number that is divisible by 3 or 5 (I found a pattern that the most divisible triangle numbers were divisible by 3 or 5)
Go through primes and divide number by primes until number equals 1
Convert the prime factors to divisors
Go to step 1 and repeat until divisors are greater than 500

While this method is more complex, it yielded great results. Once I was done refining this method, I got the compute time down to .086 seconds. That is a very substantial improvement!

The interesting part of the code is the findDivisors function, seen below.

int findDivisors(int input, int *primes, int primesToFind)
{
    int i, count=1;
    int primeCount[primesToFind];
    for (i=0; i<primesToFind; i++)
    primeCount[i] = 0;

    // Prime factorization
    while (input != 1)
        for (i=0; i<primesToFind; i++)
            if (input % primes[i] == 0)
            {
                input = input / primes[i];
                primeCount[i]++;
            }

    // Convert prime factorization to divisors
    for (i=0; i<primesToFind; i++)
        if (primeCount[i] > 0)
            count *= (primeCount[i]+1);

    return count;
}

In this function, the inputs are:

The triangle number (input)
The array of pre-calculated prime numbers (primes)
The number of primes in the array (primesToFind)

As the division of primes occurs, I keep track in a separate array (primeCount) how many times a given prime index is used to divide. This keeps track of the prime factorization I talked about earlier so we can finally compute the number of divisors. Once computed, we pass back the count, and the program moves on to the next triangle number.

So there you have it. My entire solution is available on my GitHub page.

Emacs on Mac OS X

At work I use a Linux work station a lot, and one of the things I really enjoy is that when I use Emacs from the command line, it opens up the graphical user interface. This, of course, is not the behavior on OS X. Additionally, the version that ships with Mac OS X is woefully out of date (version 22.1.1 at the time of writing).

I decided to do something about it, and grabbed an up-to-date build of Emacs from emacsformacosx.com. By default, it gets installed in /Applications, which will work just fine. It provides a graphical version of Emacs with support for normal Mac OS X short cuts, like command-c, etc.

But, Michael, how does this solve the problem of the Emacs from the command line being out of date? Well, Inside the application bundle is the Emacs executable that can be run from the command line, sans GUI. All you have to do is create an alias with this code (in my case, I made a bash script that resides in my ~/.bin named ’emacs’) with the following code:

#!/bin/sh
if
    [ -z "$SSH_CONNECTION" ]
then
    /Applications/Emacs.app/Contents/MacOS/Emacs "$@"
else
    /Applications/Emacs.app/Contents/MacOS/Emacs -nw "$@"
fi

This makes it so that if the terminal detects that you are running over an SSH (non-graphical) connection, it will run the non-windowed version of Emacs, otherwise it will launch the graphical version. It works just like it does in most Linux distros, and is a real pleasure to use!